Эта статья была прислана нам спортсменом — любителем из Сибири (г.Междуреченск) О физике поворота ведется много разговоров и нам показалось интересным разместить данный материал у нас на сайте. Предвидим вопросы и комментарии но не уверены, что сможем на них квалифицированно ответить. Поэтому предлагаем все вопросы обращать непосредственно к автору у нас в конференции или напрямую
Каждый горнолыжник знает, что чем больше закантована загруженная лыжа, тем меньшим окажется радиус поворота, который она опишет без проскальзывания. Лыжа, поставленная на кант, прогнется до тех пор, пока весь кант не получит опору на поверхность. Образующаяся при этом так называемая «дуга прилежания канта» будет определять соответствующий углу закантовки радиус поворота.
Также всем известно, что в движении при незначительной ширине опоры, будь то на горных лыжах, велосипеде или просто при ходьбе, для выполнения поворота необходимо первоначальное смещение центра масс к центру поворота (наклон) и последующее поддержание равновесия за счет опоры на поверхность. При этом возникает центростремительная сила, которая и будет изменять траекторию центра масс.
То, что более сильный наклон нужен для поддержания равновесия и для прогиба лыж в более крутую дугу очевидно, но какова динамика этих процессов, как подобрать геометрию лыж, наилучшим образом подходящих для поддержания равновесия при заданной скорости и радиусах поворота на горизонтальной поверхности — для этого потребуются совсем несложные расчеты.
Сразу оговорюсь, что ниже будет в основном несложная геометрия, и если это покажется совсем не интересным, я не несу ответственности за «зря потраченное время».
Итак, начнем.
Первоначально надо определить принятые упрощения — поверхность жесткая и ровная, а встроенная в лыжу форма дуги прилежания канта — дуга окружности, а не какая-либо другая кривая. Лыжа достаточно легко гнется в продольном направлении из-за малой толщины, но очень жесткая на изгиб в боковом направлении из-за большой ширины, можно сделать достаточно простую модель, просто вырезав ее из бумаги.
Длина дуги прилежания при постановке лыжи на кант не изменяется, изменяется лишь ее форма, всегда представляющая дугу окружности большего или меньшего радиуса,для наглядности достаточно вспомнить форму выкройки для склеивания усеченного конуса.

Представим, что мы вырезали из бумаги заштрихованную фигуру, малый радиус которой имитирует «дугу прилежания» канта лыжи, и положив ее на стол, начали приподнимать край со стороны большего радиуса, сохраняя контакт «дуги прилежания» с поверхностью стола — мы будем получать часть перевернутого усеченного конуса, при этом «дуга прилежания» будет изменять свой радиус в меньшую сторону.
Представим теперь, что мы вырезали не усеченный, а полный конус, то есть кусочек, обозначенный пунктиром, не отрезался, но сворачивать его будем, представляя, что он пересекается плоскостью по малому радиусу заштрихованной области. И что же? Перевернутый конус сворачивается точно так же, при этом вершина уходит вниз, а ее проекция на плоскость будет в центре нового радиуса дуги прилежания.
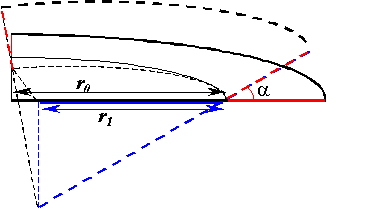
Каков будет радиус дуги прилежания в зависимости от угла между боковой поверхностью нашего конуса и горизонтальной плоскостью легко вычислить по формуле r1=r0*cos(a)
где r1 — радиус поворота заканованной лыжи,
r0 — встроенный радиус поворота плоской лыжи,
a — угол закантовки.,
Соответственно, необходимый угол закантовки вычисляется следующим образом:a=arccos(r1 / r0)
Например, при угле закантовки 60о встроенный радиус лыжи уменьшится ровно вдвое, а для сгибания лыжи, со встроенным радиусом 22 м в дугу радиусом 5 м потребуется закантовать ее на угол около 77о.
Как известно скорость, радиус поворота и центростремительное ускорение связаны между собой следующим образом: Aцентр=v2/R
где v — скорость,
R — радиус поворота,
Aцентр — центростремительное ускорение
Зависимость центростремительного, или тангенциального ускорения от угла наклона линии, проходящей через центр масс и точку опоры выражается формулой Aцентр=g*tg(a);
где g — ускорение свободного падения, 9.8 м/с2
a — угол наклона центра масс.
Из этих двух формул получаем третью, для вычисления необходимого угла наклона центра масс в зависимости от скорости и радиуса поворота: a=arctg(v2/R/g)
Ниже приведены графики необходимых углов закантовки, и углов «заклона корпуса», полученные по вышеописанным формулам, для ряда различных «встроенных радиусов поворота» R (сплошные линии) и различных скоростей движения V (пунктирные линии) при изменении радиуса поворота от 50 до 1 метра:
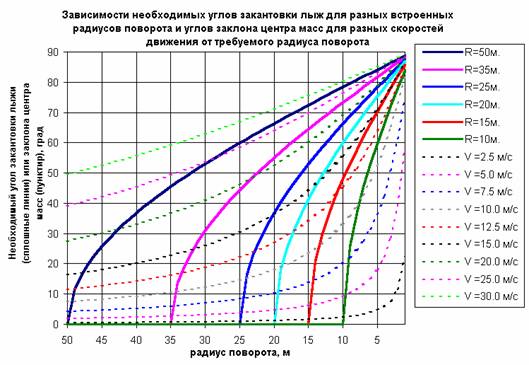
Из графиков хорошо видны «точки равновесия» — точки пересечения сплошных и пунктирных линий, например, лыжа с «встроенным радиусом» 25 м (сплошная синяя линия) при ведении дуги радиусом 20 метров на скорости 15 м/с (пунктирная черная линия) не потребует дополнительной закантовки путем сгибания в бедре или колене, а вот на скорости 12,5 м/с (пунктирная красная линия) потребуется дополнительно к углу заклона корпуса увеличить угол закантовки при помощи бедра и (или) колена почти на 10 градусов.
Конечно, эта статья лишь отчасти объясняет работу лыжи во время ведения поворота, здесь не рассматривается динамика движений, например вертикальное перемещение центра масс, которое потребует для замедления его движения вниз большей закантовки, чем для поддержания статичного равновесия, но все же думаю ее стоит прочитать лыжникам, старающимся не только нащупать равновесие в резаном повороте, но и понять, какие скорости и углы закантовки потребуются для конкретной пары лыж, и почему на высокой скорости на относительно «прямых» лыжах зачастую равновесие нащупать проще, чем на низкой.
Александр Ревкуц











